
Aperture 20 (photo: A. Pratzner)
- Camera:
- Canon EOS 5D
- Aperture :
- f/9
- Exposure:
- 1/200 Sek.
- ISO:
- 100
- Focal length:
- 70 mm
The Aperture (Shutter) is the
design element No. 1
The aperture is the mechanical mechanism in the objective, which controls the width of the objective aperture. It uses a bladed shutter to increase or decrease the opening.
When I speak about the aperture I mean the opening in the objective, which regulates the amount of light that can enter the camera through a partial closure of the opening.
In the picture above, you can see a nearly closed aperture in an objective of a SLR camera. You can easily spot the lamellae.
Operating principle of the aperture
To understand the operating principle of the aperture we take a look at the procedure when taking a photo.
| Procedure | Action of the aperture |
|---|---|
| We look through the viewfinder and decide on a section we want to photograph. After slightly pressing the trigger the camera focusses on it. | The widest aperture - the aperture is completely opened, so that as much light as possible can be used by the viewfinder and therefore the photographer can easily set a section and the sharpness. |
| It is not mandatory necessary: When we only want to control the sharpness (depth of field) for the set aperture, for that we can slightly press the trigger. | When you press the depth-of-field preview button, then the aperture will be closed according to the set value (if necessary). |
| We push through the shutter button to take a photo. | The aperture gets closed according to the set value (only if the widest aperture has not been set). |
| The curtain, which covers the image sensor, opens for the set time to expose it to the light, afterwards it closes again. | |
| The aperture resets to its initial position, which is the widest aperture. | |
| The image gets saved and can be viewed and controlled on the display of the digital camera. |
Table: technical process when taking a picture and the related action of the aperture
The aperture closes according to the set aperture value, so, only when pressing the trigger, henceforth a photo is taken - we can speak of a "working aperture". As long as you look through the viewfinder, the aperture is completely opened. Then we can speak of the "widest aperture" viz. "setting orifice". That is the case, because while setting the section and sharpness of the picture while looking through the viewfinder you want a very bright image for better adjustment.
What is the aperture good for?
The aperture controls how much light can fall onto the image sensor. The image sensor needs an appropriate amount of light to capture an image - i.e.: to take a correctly exposed photo. When the final picture is too bright, then it is overexposed. Thus, too much light could fall onto the image sensor. When the final picture is too dark, then too less light could fall onto the image sensor. But, how do we know how much light we need for a correctly exposed photo? For that, take a look at the chapter about the "correctly exposed photo".
Now, we could come to the solution, that it would be an ideal choice, when we would always take photos with the widest aperture. But the aperture has another optical characteristic. The opening of the aperture determines the depth of field of a photo.
For instance, when taking a portrait photo with the widest aperture it can happen that the eyes are sharp, but the nasal tip and ears become blurred.
That means, the aperture has the interdependence:
- The further the aperture is opened, the less depth of field there is.
- The further the aperture is closed, the more depth of field there is.
More about the topic depth of field in the comprehensive chapter about the depth of field.
So the width of the aperture is a huge design element. Because it directs the view of the observer. If a red or yellow street sign or a person looking directly into the camera it is visible in the background, every observer looks at it and not at what you have photographed. If you blur it with an reduced depth of field, the view of the observer redirects onto what you wanted as the center of the photo.
Let us take a look into the numbers and their meaning to clarify the examples.
F-numbers
In common parlance the term aperture is sometimes used as the f-number.
Every objective has generally numbers printed on it.

Fixed focal length 50 mm with f/1,4 (on the right in the picture: 1:1.4)
Here we have an objective with a focal length of 50 mm (about focal length see the chapter about objectives) and a focal ratio of 1:1,4. Common parlance speaks of an "aperture 1,4" . A correct short notation of the focal ratio would be f/1,4.
In the picture above the aperture is opened to its maximum, i.e. opened till its f-number f/1,4. A lot of light can fall through the objective.
In the following picture you can see the same objective. However, its aperture got closed till a f-number of 8. The on the objective printed value of f/1,4 is the value, how much light can maximal fall through the objective. Fewer is always possible, i.e. the aperture can always be closed.

Fixed focal length 50 mm set on the f-number 8
The f-number is the reciprocal value of the ratio between the effective opening (D) and the focal length (in the following illustration focal distance).
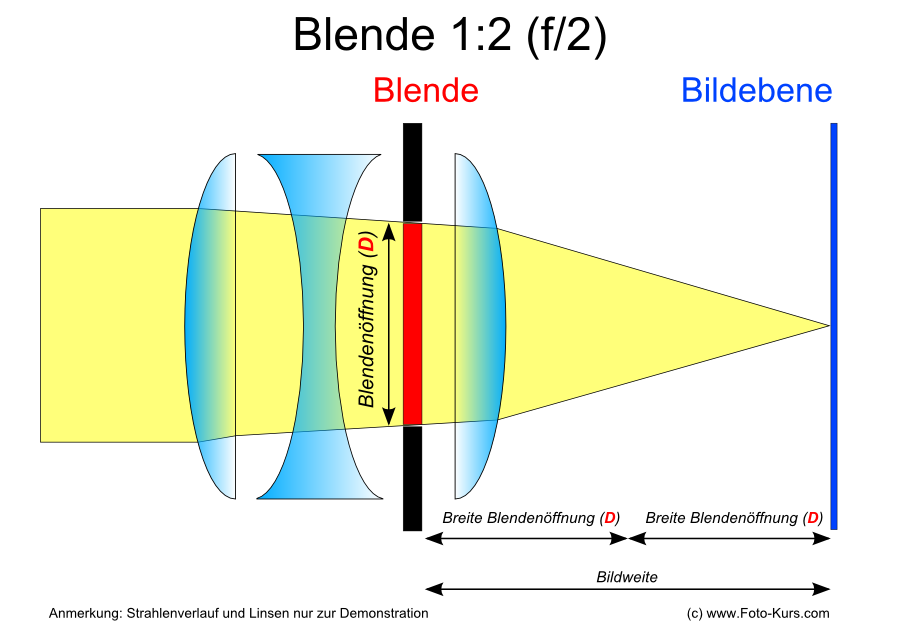
How we achieve the aperture value f/2 - focal length divided through effective opening (D)
In the illustration we can see, how the aperture opening and the focal length (so, the distance between the lense and the image plane) determine the aperture value. The illustration and the statement "the distance between the lense and the image plane" are simplifications which depict the complex issue understandable. If you want to know it exactly look up the term "effective opening". It is, in my opinion, only necessary for people who construct objectives, but not for photographers, who only need to grasp the essence of it.
The f-number is the relative aperture of the objective towards the focal length.
It refers to the relation between aspect ratio (below the fraction line) and the effective opening (that is: the at the moment aperture setting) above the fraction line (a mathematician would speak about numerator and denominator of a fraction) That is the reason of the phenomenon, that a closing of the aperture (an increasingly smaller aperture opening) the aperture value becomes ever greater.
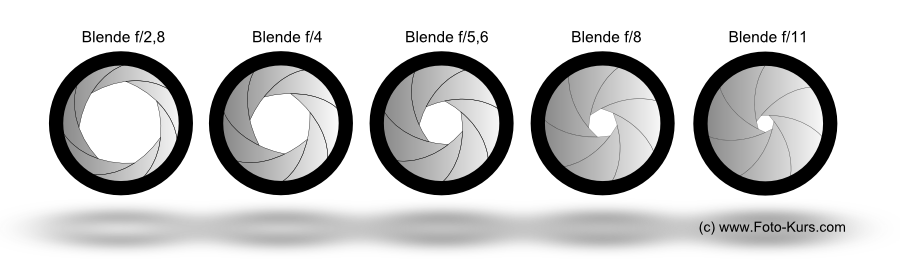
Figure: f-numbers and the size of the aperture opening
Additionally, there is the spoken short form (aperture 11), what means the aperture value f/1:11, this can lead to confusion among beginners. Best remember: the smaller the aperture value, the less depth of field does the finished picture have. This is what matters in the end for image composition - more about it in the chapter about depth of field.
Aperture value big -> aperture opening small -> little light
Explained in depth, when setting a bigger aperture value, then the aperture opening is smaller and fewer light passes through the opening. The smaller aperture opening "fits" more often in the space between aperture and image plane (sketched in the figure below). The next example is with an aperture value/ f-number of f/3,5. Let us assume the aperture opening of this objective is 10 mm and the distance between the aperture opening and the image plane is 35 mm.
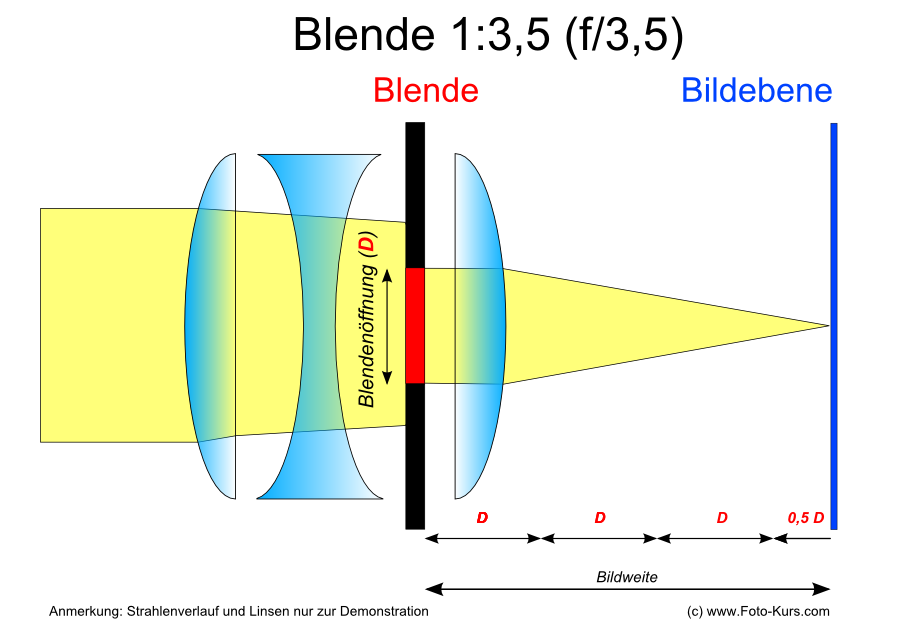
dimmed out - the aperture opening fits 3,5 times into the image plane - aperture f/3,5
Then we calculate
aperture value=10 mm/35 mm=0,2857= 1:3,5
The calculated result is 0,2857. The numbers smaller 1 are inconvenient, that is why we leave it as a fracture, i.e. 1:3,5 (without a unit).
Aperture value without a dimension
The length specification mm cancels itself out. So, we have a dimensionless number - therefore the different objectives can be easily compared to each other.
Comparable with f-numbers
Important is: the f-number f/4 always lets the same amount of light enter, no matter what objective is used. That means, when using a wide-angle lens and setting a f-number of f/4 the same amount of light will pass through as when using a telephoto lens and setting the f-number to f/4. Thus, as soon as a photographer has built up the needed experience he can use every objective and the result is assessable based on his experience. A photographer does not have to start from the bottom when acquiring a new objective, he can always rely on his experiences.
Common notations for the aperture
Common notations for the f-number are for example:
- f/2,8
- 1:2,8
- 1/2,8
- f/2,8
- F 2,8
In this photography course we will use the notation aperture value f/2,8 - this notation may be extensive and a doubling. But it should help avoid misunderstandings.
Zoom lenses with aperture specification from - to
Take a look at your objective. When there is something written like 18-250 mm 1:3.5-6.3, then do not let yourself get confused! Zoom lenses do have a variety of focal length with differing widest maximum possible apertures. In this example when setting the focal length of this objective to 18 mm, then the widest possible aperture is f/3,5 and when using a focal length of 250 mm then the widest possible aperture is f/6,3.
Only high-end objectives allow the same aperture over the whole zoom range. This is always a question of money and weight. A uniform aperture needs appropriate "glass" of high quality and space and is therefore in general heavier.
Terminology: Fade-in and Fade-out
Fade-out means the closing of the aperture. Consequently, fewer light can enter. Many objectives reach their highest image performance, when the photographer fades-out 2 aperture stops (see chapter about "critical aperture").
What is a light-intense objective?
The smaller the f-number (i.e. f/2,0 is better than f/2,8), the more light-intense is the objective. Light-intense objectives are technical much easier realizable with fixed focal length than with zoom lens. A light-intense objective can work with fewer light and still achieve a good exposure.
1.4, 2.0, 2.8, 4, 5.6, 8 - were do the leaps in the f-numbers have their origin?
Often you stumble upon the following numerical series
1.4, 2.0, 2.8, 4, 5.6, 8, 11, 16, 22, 32, 45

Aperture openings from f/2,8 to f/11 in comparison
f/2,0 has double the size of f/2,8 - double the amount of light can enter through the opening! The strange values come from the fact that the opening is a circle.
Shortly recalculated:
2 * √2=2*1,414=2,828 (rounded f-number f/2,8)
and the next f-number after f/2,8
2,8* √2=3,959 (rounded f-number f/4)
1 f-stop interval more = halving the amount of light/ 1 f-stop interval fewer = doubling the amount of light
What is the advantage of knowing, that these values correspond to a doubling/ halfing of the amount of light? We can calculate the needed time when using another f-number.
Assumption: a correctly exposed photo needs on a certain light situation a f-number of f/4 and an exposure time of 1 second.
If I want more depth of field and therefore increase my aperture to f/5,6 to take the picture (I halve the amount of light, that can fall through the aperture opening) but would not change the exposure time and leave it as 1 second, then the photo will get underexposed (too dark). I need to adjust the values to achieve a correctly exposed photo and therefore also have to double the exposure time to 2 seconds.
The camera does this automatically when using the mode P, as soon as the photographer changes the values - the camera adjusts. Setting a bigger f-number will make the camera adjust the exposure time by decreasing it and the other way round.
Task: Standing an exposure time of 1 second by hand is nearly impossible without jiggling the camera and blurring the picture. Which f-number should you choose, when you want to take the picture out of the hand with a focal length of 80 mm?
Setting the camera to apertures
Using a Canon camera adjust the camera to the setting Av (aperture priority). Now you can choose the aperture yourself and the for this light situation appropriate shutter speed (exposure time) is automatically set by the camera.

Setting Av for aperture priority
Aperture and depth of field
What do I need the depth of field for? Wouldn´t it be good, if everything would be always sharp?
In the scientific area it is sometimes desired that everything is sharp from top to bottom. On the other hand, in the artistic area and in general it is undesirable. You want to channel the view of the observer. This can all be achieved by using sharpness and blurriness. The irrelevant elements of the pictures are blurred (till no longer recognizable), the important ones are sharp. Take a look at the following pictures with a spider, a net and a background.

Spider sharp and background sharp (Photo: A. Pratzner)
- Camera:
- Canon EOS 350D
- Aperture:
- f/36
- Exposure:
- 3,2 Sek.
- ISO:
- 100
- Focal length:
- 55 mm
In the first picture everything is sharp. The observer cannot grasp, what might be important. The foreground and background are hard to separate.
In the second picture with the same spider the background became blurred through a different choice of aperture. The view of the observers is channeled onto the for the photographer important picture element (which is depicted sharp) and does not get distracted by the background.

Channeling of the view onto the spider through sharpness and a blurred background (Photo: A. Pratzner)
- Camera:
- Canon EOS 350D
- Aperture:
- f/5,6
- Exposure:
- 1/40 Sek.
- ISO:
- 400
- Focal length:
- 55 mm
The depth of field is also depending on the distance of the photographer towards the photo scene and the size of the image sensor. More about it in the chapter about depth of field.
Critical Aperture
Let us now head to an advanced field of the aperture. That it does not get so easy: Small aperture values also have like big aperture values aberrations/ imaging errors.
Source of error aberration
Optical aberration (Aberration) are deviations from the ideal optical depiction. There are a lot of different errors: from image vault errors till defects in color (chromatic aberration) and defocus. The smaller the f-numbers the more aberration errors occur.
Source of error diffraction blur
The smaller the aperture opening (big f-number), the more diffraction blur (decrease in sharpness) occurs.
Diffraction blur occurs, when the light beam gets deflected.
When we draw both blur defects in a diagram, we get a point of intersection which promises the best optical result. This point is called the critical aperture.
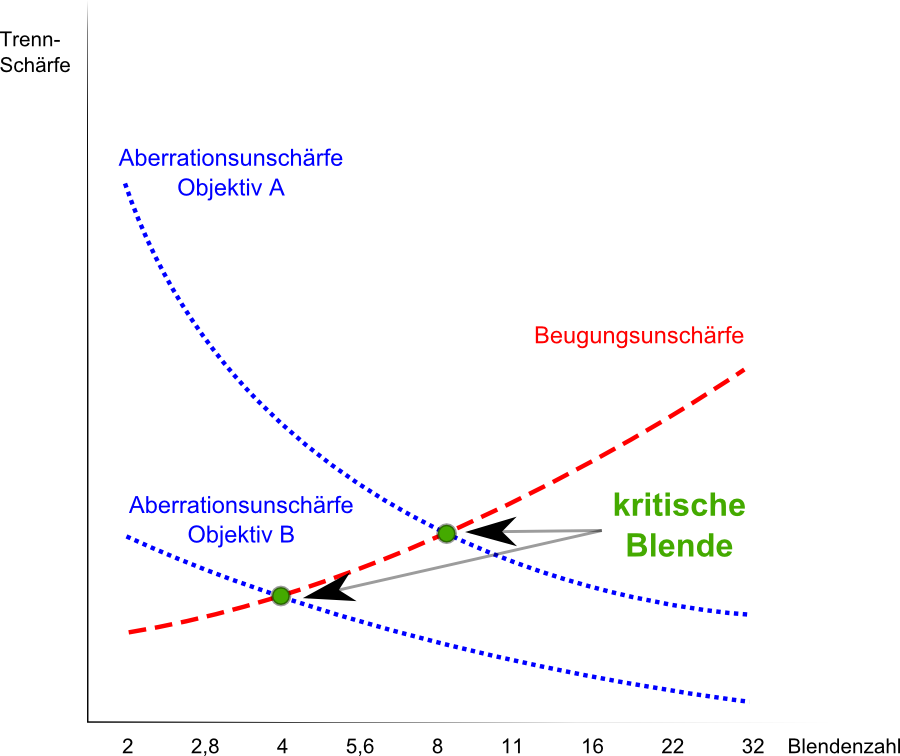
Critical aperture as a compromise between sources of error
Critical aperture = the best optical result
The critical aperture is a compromise between errors of aberration and errors of diffraction blur. It differs depending on the objective (what explains the differences in their price) Amateurs may recognize the differences by looking very precisely on a computer monitor (On a camera display it is because of the small dimension impossible to assess) Certainly, errors will be clearly visible when enlarging the images. Latest on the size of a billboard the errors are clearly visible even for the untrained eye.
Terms around the aperture
Aperture:
the mechanical construction which varies the size of the opening, through which light can enter.
Widest Aperture:
The widest aperture opening of an objective.
Aperture Ratio:
Ratio between effective opening D and the focal length f.
Common Notations:
- 1:1,4
- 1/1,4
- f/1,4
- F 1,4
f-number:
(relativ values) reciprocal of the aperture ratio is the f-number.
Typical values of f-numbers:
1,4 2 2,8 4 5,6 8 11 16 22 32
halved f-number intervals:
f/ 1,0 1,2 1,4 1,7 2 2,4 2,8 3,4 4 4,8 5,6 6,7 8 9,5 11 13 16 19 22
divided into thirds f-number intervals:
f/ 1,0 1,1 1,2 1,4 1,6 1,8 2 2,2 2,5 2,8 3,2 3,5 4 4,5 5,0 5,6 6,3 7,1 8 9 10 11 13 14 16 18 20 22 25 28 32
Aperture series:
Stops from f-number to f-number doubles/ halves the amount of light.
fade-out/ fade to black:
You choose a higher f-number, i.e. the aperture becomes smaller and fewer light falls through.
light intensity:
The initial opening of the aperture corresponds to the light intensity of the objective.